Bạn đang tìm kiếm Giải bài 11, 12, 13, 14, 15 trang 74, 75 SGK toán 8 tập 1 2023 phải không? Xin chúc mừng bạn đã tìm đúng chỗ rồi! Hãy đọc ngay bài viết dưới đây của Tekmonk
Giải bài tập trang 74, 75 bài 3 Hình thang cân sgk toán 8 tập 1. Câu 11: Tính độ dài các cạnh của hình thang cân ABCD…
Bài 11 trang 74 sgk toán 8 tập 1
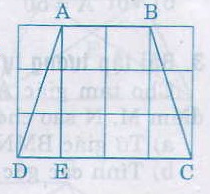
Tính độ dài các cạnh của hình thang cân ABCD trên giấy kẻ ô vuông (h.30, độ dài cạnh ô vuông là 1cm).
Bài giải:
Theo hình vẽ, ta có: AB = 2cm, CD = 4cm
Trong tam giác vuông AED, áp dụng định lý Pitago ta được:
AD2 = AE2 + ED2
= 32 + 12 =10
Suy ra AD = (sqrt{10})cm
Vậy AB = 2cm, CD = 4cm, AD = BC = (sqrt{10})cm
Bài 12 trang 74 sgk toán 8 tập 1
Cho hình thang cân ABCD ( AB // CD, AB
Bài giải:
Xét hai tam giác vuông AED và BFC
Ta có: AD = BC (gt)
(gt)
Nên ∆AED = ∆BFC (cạnh huyền – góc nhọn)
Suy ra: DE = CF
Bài 13 trang 74 sgk toán 8 tập 1
Cho hình thang cân ABCD (AB // CD), E là giao điểm của hai đường chéo. Chứng minh rằng EA = EB, EC = ED.
Bài giải:
Do ABCD là hình thang cân nên AD = BC, AC = BC, (widehat{D}=widehat{C})
Xét hai tam giác ADC và BCD, ta có:
AD = BC (gt)
AC = BD (gt)
DC chung
Nên ∆ADC = ∆BCD (c.c.c)
Suy ra (widehat{C_{1}}=widehat{D_{1}})
Do đó tam giác ECD cân tại E, nên EC = ED
Ta lại có: AC = BD suy ra EA = EB
Chú ý: Ngoài cách chứng minh ∆ADC = ∆BCD (c.c.c) ta còn có thể chứng minh ∆ADC = ∆BCD (c.g.c) như sau:
AD = BC, (widehat{D}=widehat{C}) , DC là cạnh chung.
Bài 14 trang 75 sgk toán 8 tập 1
Đố. Trong các tứ giác ABCD và EFGH trên giấy kẻ ô vuông (h.31), tứ giác nào là hình thang cân? Vì sao?
Bài giải:
Để xét xem tứ giác nào là hình thang cân ta dùng tính chất
“Trong hình thang cân hai cạnh bên bằng nhau”
Tứ giác ABCD là hình thang cân vì có AD = BC.
Tứ giác EFGH không là hình thang cân vì EF > GH.
Bài 15 trang 75 sgk toán 8 tập 1
Cho tam giác ABC cân tại A. Trên các cạnh bên AB, AC lấy theo thứ tự các điểm D và E sao cho AD = AE.
a) Chứng minh rằng BDEC là hình thang cân.
b) Tính các góc của hình thang cân đó, biết rằng (widehat{A})=500
Bài giải:
a) Ta có AD = AE nên ∆ADE cân
Do đó (widehat{D_{1}}) = (widehat{E_{1}})
Trong tam giác ADE có: (widehat{D_{1}}) + (widehat{E_{1}}) + (widehat{A})=1800
Hay 2(widehat{D_{1}}) = 1800 – (widehat{A})
(widehat{D_{1}}) = (frac{180^{0}-widehat{A}}{2})
Tương tự trong tam giác cân ABC ta có (widehat{B}) = (frac{180^{0}-widehat{A}}{2})
Nên (widehat{D_{1}}) = (widehat{B}) là hai góc đồng vị.
Suy ra DE // BC
Do đó BDEC là hình thang.
Lại có (widehat{B}) = (widehat{C})
Nên BDEC là hình thang cân.
b) Với (widehat{A})=500
Ta được (widehat{B}) = (widehat{C}) = (frac{180^{0}-widehat{A}}{2}) = (frac{180^{0}-50^{0}}{2}) = 650
(widehat{D_{2}}=widehat{E_{2}})=1800 – (widehat{B})= 1800 – 650=1150
chinese.com.vn/giao-duc
Bạn đang đọc : Giải bài 11, 12, 13, 14, 15 trang 74, 75 SGK toán 8 tập 1 2023 được cập nhập bởi Tekmonk.
Thông tin và kiến thức về chủ đề Giải bài 11, 12, 13, 14, 15 trang 74, 75 SGK toán 8 tập 1 2023 do Học viện Công nghệ Tekmonk chọn lọc và tổng hợp cùng với các chủ đề liên quan khác.
Tham khảo thêm các khóa học công nghệ đỉnh cao tại: Học viện công nghệ Tekmonk 
Nguồn: Internet
Bạn đang tìm kiếm Giải bài 1, 2, 3, 4 trang 100 Vở
Bạn đang tìm kiếm Cảm nhận bài thơ Đoàn thuyền
Bạn đang tìm kiếm Vật lý 9 bài 25: Sự nhiễm từ
Bạn đang tìm kiếm 4 Đề đọc hiểu Đây thôn Vĩ
