Bạn đang tìm kiếm Giải bài 22, 23, 24 trang 158, 159 SBT Toán 8 tập 1 2023 phải không? Xin chúc mừng bạn đã tìm đúng chỗ rồi! Hãy đọc ngay bài viết dưới đây của Tekmonk
Giải bài tập trang 158, 159 bài 2 diện tích hình chữ nhật Sách bài tập (SBT) Toán 8 tập 1. Câu 22: Cho hình bình hành ABCD (h. 184). Đường phân giác của các góc A và C cắt đường chéo BD tại E, F…
Câu 22 trang 158 Sách bài tập (SBT) Toán 8 tập 1
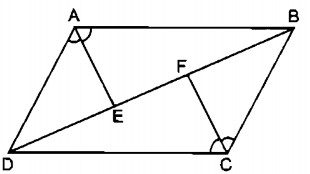
Cho hình bình hành ABCD (h. 184). Đường phân giác của các góc A và C cắt đường chéo BD tai E, F.
a. Chứng minh rằng hai hình ABCFE và ADCFE có cùng diện tích.
b. Các hình đó có phải đa giác lồi ko ? Vì sao ?
Giải:
∆ ABE = ∆ CDF (g.c.g)
( Rightarrow {S_{ABE}} = {S_{CDF}}) (1)
Ta có: ∆ AED = ∆ CFB (g.c.g)
( Rightarrow {S_{AED}} = {S_{CFB}}) (2)
Từ (1) và (2) suy ra:
({S_{ABE}} + {S_{CFB}} = {S_{CDF}} + {S_{AED}})
Hay ({S_{ABCFE}} = {S_{ADCFE}})
b. Hình ABCFE không phải đa giác lồi vì nó nằm trên hai nửa mặt phẳng có bờ là đường thẳng chứa cạnh EF.
Hình ADCFE không phải là đa giác lồi vì nó nằm trên hai nửa mặt phẳng có bờ là đường thẳng chứa cạnh EF.
Câu 23 trang 158 Sách bài tập (SBT) Toán 8 tập 1
Trên hình 185, các tứ giác ABCD và EFCH đều là hình bình hành. Điểm E nằm trên đường chéo AC.
a. Chứng minh rằng đa giác AEHD và hình ABCFE có cùng diện tích.
b. ABCFE có phải là đa giác lồi không ? Vì sao ?
Giải:
a. Ta có: ∆ ABC = ∆ CDA (c.c.c)
( Rightarrow {S_{ABC}} = {S_{CDA}}) (1)
∆ EFC = ∆ CHE (c.c.c)
( Rightarrow {S_{EFC}} = {S_{CHE}}) (2)
Từ (1) và (2) suy ra:
({S_{ABC}} – {S_{EFC}} = {S_{CDA}} – {S_{CHE}})
Hay ({S_{ABCFE}} = {S_{AEHD}})
b. Hình ABCFE không phải tứ giác lồi vì nó nằm trên hai nửa mặt phẳng có bờ là đường thẳng chứa cạnh CF.
Câu 24 trang 159 Sách bài tập (SBT) Toán 8 tập 1
Cho một tam giác vuông cân. Chứng minh rằng tổng diện tích của hai hình vuông dựng trên hai cạnh góc vuông bằng diện tích của hình vuông dựng trên cạnh huyền(không sử dụng định lý Py-ta-go)
Giải:
Gọi S là diện tích của tam giác ABC
Hình vuông có cạnh AB chia thành hai tam giác vuông cân bằng ∆ ABC nên diện tích hình vuông cạnh AB bằng 2S
Hình vuông có cạnh AC chia thành hai tam giác vuông cân bằng ∆ ABC nên có diện tích bằng 2S
Hình vuông BC chia thành 4 hình tam giác vuông cân bằng ∆ ABC nên có diện tích bằng 4S
Vì 4S = 2S + 2S nên diện tích hình vuông dựng trên hai cạnh huyền bằng tổng diên tích hai hình vuông dựng trên hai cạnh góc vuông.
chinese.com.vn/giao-duc
Bạn đang đọc : Giải bài 22, 23, 24 trang 158, 159 SBT Toán 8 tập 1 2023 được cập nhập bởi Tekmonk.
Thông tin và kiến thức về chủ đề Giải bài 22, 23, 24 trang 158, 159 SBT Toán 8 tập 1 2023 do Học viện Công nghệ Tekmonk chọn lọc và tổng hợp cùng với các chủ đề liên quan khác.
Tham khảo thêm các khóa học công nghệ đỉnh cao tại: Học viện công nghệ Tekmonk 
Nguồn: Internet
Bạn đang tìm kiếm Giải bài 1, 2, 3, 4 trang 100 Vở
Bạn đang tìm kiếm Cảm nhận bài thơ Đoàn thuyền
Bạn đang tìm kiếm Vật lý 9 bài 25: Sự nhiễm từ
Bạn đang tìm kiếm 4 Đề đọc hiểu Đây thôn Vĩ
