Bạn đang tìm kiếm Giải bài 18, 19, 20 trang 159 SBT Toán 9 tập 2 2023 phải không? Xin chúc mừng bạn đã tìm đúng chỗ rồi! Hãy đọc ngay bài viết dưới đây của Tekmonk
Giải bài tập trang 159 bài 2 Đường kính và dây của đường tròn Sách bài tập (SBT) Toán 9 tập 2. Câu 18: Cho đường tròn (O) có bán kính OA = 3cm. Dây BC của đường tròn vuông góc với OA tại trung điểm của OA…
Câu 18 trang 159 Sách bài tập (SBT) Toán 9 Tập 1
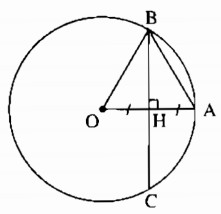
Cho đường tròn (O) có bán kính OA = 3cm. Dây BC của đường tròn vuông góc với OA tại trung điểm của OA. Tính độ dài BC.
Giải:
Gọi I là trung điểm của AB
Suy ra: (IO = IA = {1 over 2}OA = {3 over 2})
Ta có: BC ⊥OA (gt)
Suy ra: (widehat {OIB} = 90^circ )
Áp dụng định lí Pi-ta-go vào tam giác vuông OIB ta có: (O{B^2} = B{I^2} + I{O^2})
suy ra: (B{I^2} = O{B^2} – I{O^2})
(={3^2} – {left( {{3 over 2}} right)^2} = 9 – {9 over 4} = {{27} over 4})
(BI ={{3sqrt 3 } over 2}) (cm)
Ta có: BI = CI (đường kính dây cung)
Suy ra: (BC = 2BI=2.{{3sqrt 3 } over 2} = 3sqrt 3 ) (cm)
Câu 19 trang 159 Sách bài tập (SBT) Toán 9 Tập 1
Cho đường tròn (O), đường kính AD = 2R. Vẽ cung tâm D bán kính R, cung này cắt đường tròn (O) ở B và C.
a) Tứ giác OBDC là hình gì? Vì sao?
b) Tính số đo các góc CBD, CBO, OBA.
c) Chứng minh rằng tam giác ABC là tam giác đều.
Giải:
a) Ta có:
OB = OC = R (vì B, C nằm trên (O ; R))
DB = DC = R ( vì B, C nằm trên (D ; R))
Suy ra : OB = OC = DB = DC.
Vậy tứ giác OBDC là hình thoi.
b) Ta có: OB = OD = BD = R
∆OBD đều ( Rightarrow widehat {OBD} = 60^circ )
Vì OBDC là hình thoi nên:
(widehat {CBD} = widehat {OBC} = {1 over 2}widehat {OBD} = 30^circ )
Tam giác ABD nội tiếp trong (O) có AD là đường kính nên:
(widehat {ABD} = 90^circ )
Mà (widehat {OBD} + widehat {OBA} = 90^circ )
Nên (widehat {OBA} = widehat {ABD} – widehat {OBD} = 90^circ – 60^circ = 30^circ )
c) Tứ giác OBDC là hình thoi nên OD ⊥ BC hay AD ⊥ BC
Ta có: AB = AC ( tính chất đường trung trực)
Suy ra tam giác ABC cân tại A (1)
Mà (widehat {ABC} = widehat {OBC} – widehat {OBA} = 30^circ + 30^circ = 60^circ ). (2)
Từ (1) và (2) suy ra tam giác ABC đều.
Câu 20 trang 159 Sách bài tập (SBT) Toán 9 Tập 1
a) Cho nửa đường tròn tâm O, đường kính AB, dây CD. Các đường vuông góc với CD tại C và D tương ứng cắt AB ở M và N. Chứng minh rằng AM = BN.
b) Cho nửa đường tròn tâm O, đường kính AB. Trên AB lấy các điểm M, N sao cho
AM = BN. Qua M và qua N, kẻ các đường thẳng song song với nhau, chúng cắt nửa đường tròn lần lượt ở C và D. Chứng minh rằng MC và ND vuông góc với CD.
Giải:
a) Ta có: CM ⊥CD
DN⊥CD
Suy ra: CM // DN
Kẻ OI ⊥CD
Suy ra: OI // CM // DN
Ta có: IC = ID (đường kính dây cung)
Suy ra: OM = ON (1)
Mà: AM + OM = ON + BM( = R) (2)
Từ (1) và (2) suy ra: AM = BN.
b) Ta có: MC // ND (gt)
Suy ra tứ giác MCDN là hình thang
Lại có: OM + AM = ON + BN (= R)
Mà AM = BN (gt)
Suy ra: OM = ON
Kẻ OI ⊥ CD (3)
Suy ra: IC = ID (đường kính dây cung)
Khi đó OI là đường trung bình của hình thang ACDN
Suy ra: OI // MC // ND (4)
Từ (3) và (4) suy ra: MC ⊥ CD, ND ⊥ CD.
chinese.com.vn/giao-duc
Bạn đang đọc : Giải bài 18, 19, 20 trang 159 SBT Toán 9 tập 2 2023 được cập nhập bởi Tekmonk.
Thông tin và kiến thức về chủ đề Giải bài 18, 19, 20 trang 159 SBT Toán 9 tập 2 2023 do Học viện Công nghệ Tekmonk chọn lọc và tổng hợp cùng với các chủ đề liên quan khác.
Tham khảo thêm các khóa học công nghệ đỉnh cao tại: Học viện công nghệ Tekmonk 
Nguồn: Internet
Bạn đang tìm kiếm Giải bài 1, 2, 3, 4 trang 100 Vở
Bạn đang tìm kiếm Cảm nhận bài thơ Đoàn thuyền
Bạn đang tìm kiếm Vật lý 9 bài 25: Sự nhiễm từ
Bạn đang tìm kiếm 4 Đề đọc hiểu Đây thôn Vĩ
[contact-form-7 id="12" title="Contact form 1"]