Bạn đang tìm kiếm Giải bài 157, 158, 159, 160 trang 99, 100 SBT Toán 8 tập 1 2023 phải không? Xin chúc mừng bạn đã tìm đúng chỗ rồi! Hãy đọc ngay bài viết dưới đây của Tekmonk
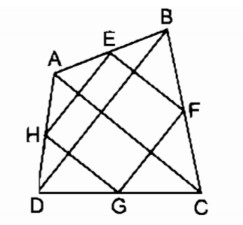
Giải bài tập trang 99, 100 bài ôn tập chương I – tứ giác Sách bài tập (SBT) Toán 8 tập 1. Câu 157: Cho tứ giác ABCD. Gọi E, F, G, H theo thứ tự là trung điểm của AB, BC, CD, DA. Tìm điều kiện của tứ giác ABCD để EFGH là…
Câu 157 trang 99 Sách bài tập (SBT) Toán 8 tập 1
Cho tứ giác ABCD. Gọi E, F, G, H theo thứ tự là trung điểm của AB, BC, CD, DA. Tìm điều kiện của tứ giác ABCD để EFGH là:
a. Hình chữ nhật
b. Hình thoi
c. Hình vuông
Giải:
Trong ∆ ABC ta có EF là đường trung bình nên EF // AC và EF = ({1 over 2})AC (1)
Trong ∆ ADC ta có HG là đường trung bình nên HG // AC và HG = ({1 over 2})AC (2)
Từ (1) và (2) suy ra: EF // HG và EF = HG
Vậy tứ giác EFGH là hình bình hành
a. Tứ giác EFGH là hình chữ nhật ⇔ EH ⊥ EF ⇔ AC ⊥ BD
b. Tứ giác EFGH là hình thoi ⇔ EH = EF ⇔ AC = BD
c. Tứ giác EFGH là hình vuông ⇔ AC ⊥ BD và AC = BD
Câu 158 trang 100 Sách bài tập (SBT) Toán 8 tập 1
Cho tam giác ABC vuông tại A, điểm D là trung điểm của BC. Gọi M là điểm đối xứng với D qua AB, E là giao điểm của DM và AB. Gọi N là điểm đối xứng với D qua AC, F là giao điểm của DN và AC.
a. Tứ giác AEDF là hình gì ? Vì sao ?
b. Các tứ giác ADBM, ADCN là hình gì ? Vì sao ?
c. Chứng minh rằng M đối xứng với N qua A
d. Tam giác vuông ABC có điều kiện gì thì tứ giác AEDF là hình vuông ?
Giải:
a. Điểm M và điểm D đối xứng qua trục AB
⇒ AB là đường trung trực của đoạn thẳng MD
⇒ AB ⊥ DM
⇒ (widehat {AED} = {90^0})
Điểm D và điểm N đối xứng nhau qua trục AC ⇒ AC là đường trung trực của đoạn thẳng DN
⇒ AC ⊥ DN ( Rightarrow widehat {AFD} = {90^0})
(widehat {EAF} = {90^0}) (gt)
Vậy tứ giác AEDF là hình chữ nhật (vì có ba góc vuông)
b. Tứ giác AEDF là hình chữ nhật ⇒ DE // AC; DF // AB
Trong ∆ ABC ta có: DB = DC (gt)
DE // AC
Suy ra: AE = EB (tính chất đường trung bình tam giác); DF// AB
Suy ra: AF = FC (tính chất đường trung bình của tam giác)
Xét tứ giác ADBM : AE = EB (chứng minh trên)
ED = EM (vì AB là trung trực DM)
Suy ra: Tứ giác ADBM là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường)
AB ⊥ DM
Vậy hình bình hành ADBM là hình thoi ( vì có hai đường chéo vuông góc)
Xét tứ giác ADCN:
AF = FC (chứng minh trên)
DF = FN (vì AC là đường trung trực DN)
Suy ra: Tứ giác ADCN là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường)
AC ⊥ DN
Vậy hình bình hành ADCN là hình thoi (vì có hai đường chéo vuông góc)
c. Tứ giác ADBM là hình thoi ⇒ AM // DB và AM = AD
hay AM // BC và AM = AD (1)
Tứ giác ADCN là hình thoi ⇒ AN // DC và AD = AN
hay AN // BC và AN = AD (2)
Từ (1) và (2) suy ra: AM trung với AN hay M, A, N thẳng hàng
Và AM = AN nên A là trung điểm của MN
Vậy điểm M và điểm N đối xứng với nhau qua điểm A
d. Hình chữ nhật AEDF trở thành hình vuông khi AE = AF
Ta có: AE = ({1 over 2})AB ; AF =({1 over 2})AC
nên AE = AF AB = AC
Vậy nếu ∆ ABC vuông cân tại A thì tứ giác AEDF là hình vuông.
Câu 159 trang 100 Sách bài tập (SBT) Toán 8 tập 1
Cho tam giác ABC vuông tại A, đường cao AH. Gọi D là điểm đối xứng với H qua AB, gọi E là điểm đối xứng với H qua AC.
a. Chứng minh rằng D đối xứng với E qua A
b. Tam giác DHE là tam giác gì ? Vì sao ?
c. Tứ giác BDEC là hình gì ? Vì sao ?
d. Chứng minh rằng BC = BD + CE.
Giải:
a. Điểm D đối xứng điểm H qua trục AB
⇒ AB là đường trung trực của HD
⇒ AH = AD (tính chất đường trung trực) ⇒ ∆ ADH cân tại A
Suy ra: AB là tia phân giác của (widehat {DAH} Rightarrow widehat {DAB} = {widehat A_1})
Điểm H và điểm E đối xứng qua trục AC
⇒ AC là đường trung trực của HE
⇒ AH = AE (tính chất đường trung trực) ⇒ ∆ AHE cân tại A
Suy ra: AC là đường phân giác của (widehat {HAE} Rightarrow {widehat A_2} = widehat {EAC})
(widehat {DAE} = widehat {DAH} + widehat {HAE} = 2left( {{{widehat A}_1} + {{widehat A}_2}} right) = {2.90^0} = {180^0})
D, A, E thẳng hàng
AD = AE (vì cùng bằng AH)
nên điểm A là trung điểm của đoạn DE
Vậy điểm D đối xứng với điểm E qua điểm A.
b) Tam giác DHE có HA là trung tuyến và (AH = {1 over 2}DE)
nên tam giác DHE vuông tại H.
c) Xét (Delta ADB) và ( Delta AHB) có:
+) AB chung
+) BD = BH ( vì AB là trung trực của DH)
+) AD = AH (vì AB là trung trực của DH)
(Rightarrow Delta ADB = Delta AHB;(c.c.c))
( Rightarrow widehat {AHB} = widehat {ADB}=90^0) (hai góc tương ứng)
Xét (Delta AEC) và ( Delta AHC) có:
+) AC chung
+) EC = HC ( vì AC là trung trực của EH)
+) AE = AH (vì AC là trung trực của EH)
(Rightarrow Delta AEC = Delta AHC;(c.c.c))
( Rightarrow widehat {AHC} = widehat {AEC}=90^0) (hai góc tương ứng)
Suy ra BD//CE (vì cùng vuông góc với DE)
Do đó tứ giác BDEC là hình thang có 2 góc vuông kề cạnh bên DE nên BDEC là hình thang vuông.
d) Do AB là đường trung trực của DH nên BD=BH (5)
Do AC là đường trung trực của EH nên CE=CH (6)
Cộng vế với vế của (5) và (6) ta có BD+CE=BH+CH hay BD+CE=BC
Câu 160 trang 100 Sách bài tập (SBT) Toán 8 tập 1
Cho tứ giác ABCD. Gọi E, F, G, H theo thứ tự là trung điểm của AB, AC, DC, DB. Tìm điều kiện của tứ giác ABCD để EFGH là:
a. Hình chữ nhật
b. Hình thoi
c. Hình vuông
Giải:
Xét tam giác ABC:
Ta có: EB = EA, FA = FC (gt)
Nên EF // BC, EF = ({1 over 2}) BC.
Xét tam giác BDC có
HB = HD, GD = GC (gt)
Nên HG // BC, HG = ({1 over 2}) BC.
Do đó EF //HG, EF = HG.
Tương tự EH // FG, EH = FG
Vậy EFGH là hình bình hành.
a) EFGH là hình chữ nhật ⇔ EH ⊥ EF ⇔ AD ⊥ BC
b) EFGH là hình thoi ⇔ EH = EF ⇔ AD = BC
c) EFGH là hình thoi ⇔ AD ⊥ BC và AD = BC
chinese.com.vn/giao-duc
Bạn đang đọc : Giải bài 157, 158, 159, 160 trang 99, 100 SBT Toán 8 tập 1 2023 được cập nhập bởi Tekmonk.
Thông tin và kiến thức về chủ đề Giải bài 157, 158, 159, 160 trang 99, 100 SBT Toán 8 tập 1 2023 do Học viện Công nghệ Tekmonk chọn lọc và tổng hợp cùng với các chủ đề liên quan khác.
Tham khảo thêm các khóa học công nghệ đỉnh cao tại: Học viện công nghệ Tekmonk 
Nguồn: Internet
Bạn đang tìm kiếm Giải bài 1, 2, 3, 4 trang 100 Vở
Bạn đang tìm kiếm Cảm nhận bài thơ Đoàn thuyền
Bạn đang tìm kiếm Vật lý 9 bài 25: Sự nhiễm từ
Bạn đang tìm kiếm 4 Đề đọc hiểu Đây thôn Vĩ
