Bạn đang tìm kiếm Giải bài 16, 17, 18, 19 trang 75 SGK toán 8 tập 1 2023 phải không? Xin chúc mừng bạn đã tìm đúng chỗ rồi! Hãy đọc ngay bài viết dưới đây của Tekmonk
Giải bài tập trang 75 bài 3 Hình thang cân sgk toán 8 tập 1. Câu 16: Cho tam giác ABC cân tại A, các đường phân giác BD, CE…
Bài 16 trang 75 sgk toán 8 tập 1
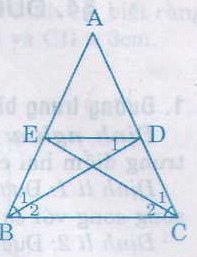
Cho tam giác ABC cân tại A, các đường phân giác BD, CE (D ∈ AC, E ∈ AB). Chứng minh rằng BEDC là hình thang cân có đáy nhỏ bằng cạnh bên.
Bài giải:
a) ∆ABD và ∆ACE có
AB = AC (gt)
(widehat{A}) chung
(widehat{B_{1}}) = (widehat{C_{1}}) (left ( =frac{1}{2}widehat{B}=frac{1}{2}widehat{C} right ))
Nên ∆ABD = ∆ACE (g.c.g)
Suy ra AD = AE
Chứng minh BEDC là hình thang cân như câu a của bài 15.
b) Vì BEDC là hình thang cân nên DE // BC.
Suy ra (widehat{_{D_{1}}}) = (widehat{B_{2}}) (so le trong)
Lại có (widehat{B_{2}}) = (widehat{B_{1}}) nên (widehat{B_{1}}) = (widehat{_{D_{1}}})
Do đó tam giác EBD cân. Suy ra EB = ED.
Vậy BEDC là hình thang cân có đáy nhỏ bằng cạnh bên.
Bài 17 trang 75 sgk toán 8 tập 1
Hình thang ABCD (AB // CD) có (widehat{ACD}=widehat{BDC}). Chứng minh rằng ABCD là hình thang cân.
Bài giải:
Gọi E là giao điểm của AC và BD.
∆ECD có (widehat{C_{1}}=widehat{D}) (do (widehat{ACD}=widehat{BDC})) nên là tam giác cân.
Suy ra EC = ED (1)
Tương tự EA = EB (2)
Từ (1) và (2) suy ra AC = BD
Hình thang ABCD có hai đường chéo bằng nhau nên là hình thang cân.
Bài 18 trang 75 sgk toán 8 tập 1
Chứng minh định lí “Hình thang có hai đường chéo bằng nhau là hình thang cân” qua bài toán sau: Cho hình thang ABCD (AB = CD) có AC = BD.
Qua B kẻ đường thẳng song song với AC, cắt đường thẳng DC tại E. Chứng mình rằng:
a) ∆BDE là tam giác cân.
b) ∆ACD = ∆BDC.
c) Hình thang ABCD là hình thang cân.
Bài giải:
a) Hình thang ABEC (AB // CE) có hai cạnh bên AC, BE song song nên chúng bằng nhau:
AC = BE (1)
Theo giả thiết AC = BD (2)
Từ (1) và (2) suy ra BE = BD do đó tam giác BDE cân.
b) Ta có AC // BE suy ra
= (3)
∆BDE cân tại B (câu a) nên
= (4)
Từ (3) và (4) suy ra
=
Xét ∆ACD và ∆BCD có AC = BD (gt)
= (cmt)
CD cạnh chung
Nên ∆ACD = ∆BDC (c.g.c)
c) ∆ACD = ∆BDC (câu b)
Suy ra
Hình thang ABCD có hai góc kề một đáy bằng nhau nên là hình thang cân.
Bài 19 trang 75 sgk toán 8 tập 1
Đố. Cho ba điểm A, D, K trên giấy kẻ ô vuông (h.32). Hãy tìm điểm thứ tư M là giao điểm của các dòng kẻ sao cho nó cùng với ba điểm đã cho là bốn đỉnh của một hình thang cân
.
Bài giải:
Có thể tìm được hai điểm M là giao điểm của các dòng kẻ sao cho nó cùng với ba điểm đã cho A, D, K là bốn đỉnh của một hình thang cân. Đó là hình thang AKDM1 (với AK là đáy) và hình thang ADKM2 (với DK là đáy).
chinese.com.vn/giao-duc
Bạn đang đọc : Giải bài 16, 17, 18, 19 trang 75 SGK toán 8 tập 1 2023 được cập nhập bởi Tekmonk.
Thông tin và kiến thức về chủ đề Giải bài 16, 17, 18, 19 trang 75 SGK toán 8 tập 1 2023 do Học viện Công nghệ Tekmonk chọn lọc và tổng hợp cùng với các chủ đề liên quan khác.
Tham khảo thêm các khóa học công nghệ đỉnh cao tại: Học viện công nghệ Tekmonk

Nguồn: Internet
Có thể bạn muốn biết:
Đã đọc:
156