Bạn đang tìm kiếm Giải bài 31, 32, 33 trang 161 SBT Toán 9 tập 2 2023 phải không? Xin chúc mừng bạn đã tìm đúng chỗ rồi! Hãy đọc ngay bài viết dưới đây của Tekmonk
Giải bài tập trang 161 bài 3 Liên hệ giữa dây và khoảng cách từ tâm đến dây Sách bài tập (SBT) Toán 9 tập 2. Câu 31: Cho đường tròn (O), các bán kính OA và OB…
Câu 31 trang 161 Sách bài tập (SBT) Toán 9 Tập 1
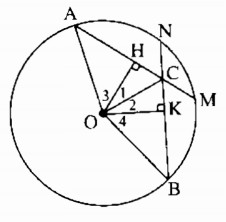
Cho đường tròn (O), các bán kính OA và OB. Trên cung nhỏ AB lấy các điểm M và N sao cho AM = BN. Gọi C là giao điểm của các đường thẳng AM và BN. Chứng minh rằng:
a) OC là tia phân giác của góc AOB.
b) OC vuông góc với AB.
Giải:
a) Kẻ OH ⊥ AM, OK ⊥ BN
Ta có: AM = BN (gt)
Suy ra: OH = OK (hai dây bằng nhau cách đều tâm)
Xét hai tam giác OCH và OCK, ta có:
(widehat {OHC} = widehat {OKC} = 90^circ )
OC chung
OH = OK (chứng minh trên)
Suy ra: ∆OCH = ∆OCK (cạnh huyền, cạnh góc vuông)
(widehat {{O_1}} = widehat {{O_2}})
Xét hai tam giác OAH và OBK, ta có:
(widehat {OHA} = widehat {OKB} = 90^circ )
OA = OB
OH = OK ( chứng minh trên)
Suy ra: ∆OAH = ∆OBK (cạnh huyền, cạnh góc vuông)
(widehat {{O_3}} = widehat {{O_4}})
Suy ra: (widehat {{O_1}} + widehat {{O_3}} = widehat {{O_2}} + widehat {{O_4}}) hay (widehat {AOC} = widehat {BOC})
Vậy OC là tia phân giác của (widehat {AOB})
b) Tam giác OAB cân tại O có OC là tia phân giác nên OC đồng thời cũng là đường cao ( tính chất tam giác cân).
Suy ra: OC ⊥ AB.
Câu 32* trang 161 Sách bài tập (SBT) Toán 9 Tập 1
Cho đường tròn tâm O bán kính 5dm, điểm M cách O là 3dm.
a) Tính độ dài dây ngắn nhất đi qua điểm M.
b) Tính độ dài dây dài nhất đi qua M.
Giải:
a) Dây đi qua M ngắn dây là dây AB vuông góc với OM.
Áp dụng định lí Pi-ta-go vào tam giác vuông OAM ta có:
(O{A^2} = A{M^2} + O{M^2})
Suy ra: (A{M^2} = O{A^2} – O{M^2} = {5^2} – {3^2} = 16)
AM = 4 (dm)
Ta có: OM ⊥ AB
Suy ra: AM = ({1 over 2}AB)
Hay: AB = 2AM = 2.4 = 8 (dm)
b) Dây đi qua M lớn nhất khi nó là đường kính của đường tròn (O). Vậy dây có độ dài bằng 2R = 2.5 = 10 (dm)
Câu 33* trang 161 Sách bài tập (SBT) Toán 9 Tập 1
Cho đường tròn (O), hai dây AB và CD cắt nhau tại điểm M nằm bên trong đường tròn. Gọi H và K theo thứ tự là trung điểm của AB và CD. Cho biết AB >CD, chứng minh rằng MH > MK.
Giải:
Ta có: HA = HB (gt)
Suy ra: OH ⊥ AB (đường kính dây cung)
Lại có: KC = KD (gt)
Suy ra: OK ⊥ CD ( đường kính dây cung)
Mà AB > CD (gt)
Nên OK > OH ( dây lớn hơn gần tâm hơn)
Áp dụng định lí Pi-ta-go vào tam giác vuông OHM ta có:
(O{M^2} = O{H^2} + H{M^2})
Suy ra: (H{M^2} = O{M^2} – O{H^2}) (1)
Áp dụng định lí Pi-ta-go vào tam giác vuông OKM, ta có:
(O{M^2} = O{K^2} + K{M^2})
Suy ra: (K{M^2} = O{M^2} – O{K^2}) (2)
Mà OH
Từ (1), (2) và (3) suy ra: (H{M^2} > K{M^2}) hay HM > KM.
chinese.com.vn/giao-duc
Bạn đang đọc : Giải bài 31, 32, 33 trang 161 SBT Toán 9 tập 2 2023 được cập nhập bởi Tekmonk.
Thông tin và kiến thức về chủ đề Giải bài 31, 32, 33 trang 161 SBT Toán 9 tập 2 2023 do Học viện Công nghệ Tekmonk chọn lọc và tổng hợp cùng với các chủ đề liên quan khác.
Tham khảo thêm các khóa học công nghệ đỉnh cao tại: Học viện công nghệ Tekmonk 
Nguồn: Internet
Bạn đang tìm kiếm Giải bài 1, 2, 3, 4 trang 100 Vở
Bạn đang tìm kiếm Cảm nhận bài thơ Đoàn thuyền
Bạn đang tìm kiếm Vật lý 9 bài 25: Sự nhiễm từ
Bạn đang tìm kiếm 4 Đề đọc hiểu Đây thôn Vĩ
[contact-form-7 id="12" title="Contact form 1"]