Giải bài 57, 58, 59, 60 trang 165, 166 SBT Toán 9 tập 2 2023

Đánh giá bài này

Bạn đang tìm kiếm Giải bài 57, 58, 59, 60 trang 165, 166 SBT Toán 9 tập 2 2023 phải không? Xin chúc mừng bạn đã tìm đúng chỗ rồi! Hãy đọc ngay bài viết dưới đây của Tekmonk

Giải bài tập trang 165, 166 bài 6 Tính chất của hai tiếp tuyến cắt nhau Sách bài tập (SBT) Toán 9 tập 2. Câu 57: Chứng minh rằng nếu tam giác ABC có chu vi 2p,bán kính đường tròn nội tiếp bằng r thì diện tích S của tam giác có công thức…

Câu 57 trang 165 Sách bài tập (SBT) Toán 9 Tập 1

Chứng minh rằng nếu tam giác ABC có chu vi 2p,bán kính đường tròn nội tiếp bằng r thì diện tích S của tam giác có công thức:

S = p.r

Giải:

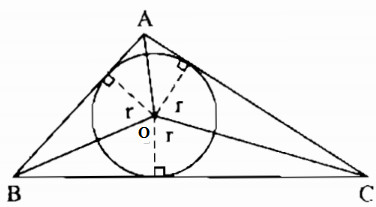
Gọi O là tâm đường tròn nội tiếp tam giác ABC

Nối OA, OB, OC.

Khoảng cách từ tâm O đến các tiếp điểm là đường cao của các tam giác OAB, OAC, OBC.

Ta có: ({S_{ABC}} = {S_{OAB}} + {S_{OAC}} + {S_{OBC}})

(= {1 over 2}.AB.r + {1 over 2}.AC.r + {1 over 2}.BC.r)

(= {1 over 2}(AB + AC + BC).r)

Mà AB + AC + BC = 2p

Nên ({S_{ABC}} = {1 over 2}.2p.r = p.r)

Loigiaihay.com

Câu 58 trang 165 Sách bài tập (SBT) Toán 9 Tập 1

Cho tam giác ABC vuông tại A. Đường tròn (O) nội tiếp tam giác ABC tiếp xúc với AB, AC lần lượt tại D, E.

a) Tứ giác ADOE là hình gì? Vì sao?

b) Tính bán kính của đường tròn (O) biết AB = 3cm, AC = 4cm

Giải:

a) Ta có: (OD bot AB Rightarrow widehat {ODA} = 90^circ )

(OE bot AC Rightarrow widehat {OEA} = 90^circ )

(widehat {BAC} = 90^circ ) (gt)

Tứ giác ADOE có ba góc vuông nên nó là hình chữ nhật

Lại có: AD = AE (tính chất hai tiếp tuyến giao nhau)

Vậy tứ giác ADOE là hình vuông.

b) Áp dụng định lí Pi-ta-go vào tam giác vuông ABC ta có:

(B{C^2} = A{B^2} + A{C^2} = {3^2} + {4^2} = 25)

Suy ra: BC = 5 (cm)

Theo tính chất tiếp tuyến giao nhau ta có:

AD = AE

BD = BF

CE = CF

Mà: AD = AB – BD

AE = AC – CF

Suy ra: AD + AE = AB – BD + (AC – CF )

= AB + AC – (BD + CF )

= AB + AC – (BF + CF )

= AB + AC – BC

Suy ra: ( AD = AE = {{AB + AC – BC} over 2} = {{3 + 4 – 5} over 2} = 1 (cm))

Câu 59 trang 165 Sách bài tập (SBT) Toán 9 Tập 1

Cho tam giác ABC vuông tại A. Gọi R là bán kính của đường tròn ngoại tiếp, r là bán kính của đường tròn nội tiếp tam giác ABC. Chứng minh rằng:

AB + AC = 2(R + r).

Giải:

Vì tam giác ABC vuông tại A nên tâm đường tròn ngoại tiếp tam giác ABC là trung điểm của cạnh huyền BC.

Ta có: BC = 2R

Giả sử đường tròn tâm (O) tiếp với AB tại D, AC tại E và BC tại F.

Theo kết quả câu a) bài 58, ta có ADOE là hình vuông.

Suy ra: AD = AE = EO = OD = r

Theo tính chất hai tiếp tuyến cắt nhau ta có:

AD = AE

BD = BF

CE = CF

Ta có: 2R + 2r = BF + FC + AD + AE

= (BD + AD) + (AE +CE)

= AB + AC

Vậy AB = AC = 2 (R + r).

Câu 60 trang 166 Sách bài tập (SBT) Toán 9 Tập 1

Cho tam giác ABC, đường tròn (K) bằng tiếp góc trong góc A tiếp xúc với các tia AB và AC theo thứ tự tại E và F. Cho BC = a, AC = b, AB = c. Chứng minh rằng:

a) (AE = AF = {{a + b + c} over 2})

b) (BE = {{a + b – c} over 2};)

c) (CF = {{a + c – b} over 2})

Giải:

a) Gọi D là tiếp điểm của đường tròn (K) với cạnh BC.

Theo tính chất hai tiếp tuyến cắt nhau ta có:

BE = BD; CD = CF

AE = AB + BE

AF = AC + CF

Suy ra: AE + AF = AB + BE + AC + CF

= AB + AC + (BD + DC)

= AB + AC + BC = c + b + a

Mà AE = AF (tính chất hai tiếp tuyến cắt nhau)

Suy ra: ({rm{AE = AF = }}{{a + b + c} over 2})

b) Ta có: (BE = AE – AB = {{a + b + c} over 2} – c = {{a + b – c} over 2})

c) Ta có: (CF = AF – AC = {{a + b + c} over 2} – b = {{a + c – b} over 2}.)

chinese.com.vn/giao-duc

Bạn đang đọc : Giải bài 57, 58, 59, 60 trang 165, 166 SBT Toán 9 tập 2 2023 được cập nhập bởi Tekmonk.

Thông tin và kiến thức về chủ đề Giải bài 57, 58, 59, 60 trang 165, 166 SBT Toán 9 tập 2 2023 do Học viện Công nghệ Tekmonk chọn lọc và tổng hợp cùng với các chủ đề liên quan khác.

Tham khảo thêm các khóa học công nghệ đỉnh cao tại: Học viện công nghệ Tekmonk

Nguồn: Internet