Bạn đang tìm kiếm Giải bài 25, 26, 27 trang 67, 68 SBT Toán 9 tập 1 2023 phải không? Xin chúc mừng bạn đã tìm đúng chỗ rồi! Hãy đọc ngay bài viết dưới đây của Tekmonk
Giải bài tập trang 67, 68 bài 5 hệ số góc của đường thẳng y = ax + b Sách bài tập (SBT) Toán 9 tập 1. Câu 25: Tìm hệ số góc của đường thẳng đi qua gốc tọa độ và đi qua điểm A(2;1)…
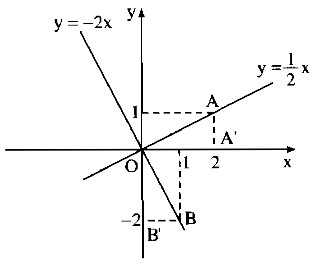
Câu 25 trang 67 Sách Bài Tập (SBT) Toán 9 Tập 1
a) Tìm hệ số góc của đường thẳng đi qua gốc tọa độ và đi qua điểm A(2;1) ;
b) Tìm hệ số của đường thẳng đi qua gốc tọa độ và đi qua điểm B(1;-2) ;
c) Vẽ đồ thị của các hàm số với hệ số góc tìm được ở các câu a) , b) trên cùng một mặt phẳng tọa độ và chừng tỏ rằng hai đường thẳng đó vuông góc với nhau.
Gợi ý làm bài:
Đường thẳng đi qua gốc tọa độ có dạng y = ax + b.
a) Vì đường thẳng y = ax + b đi qua điểm A(2;1) nên tọa độ điểm A nghiệm đúng với phương trình đường thẳng.
Ta có : (1 = a.2 Leftrightarrow a = {1 over 2})
Vậy hệ số góc mà đường thẳng đi qua gốc tọa độ và đi qua điểm A(2;1) là (a = {1 over 2}).
b) Vì đường thẳng y = ax đi qua điểm B(1;-2) nên tọa độ điểm B nghiệm đúng phương trình đường thẳng.
Ta có: 9 – 2 = a.1 Leftrightarrow a = – 2)
Vậy hệ số góc của đường thẳng đi qua gốc tọa độ và đi qua điểm B(1;-2)
Là a = -2.
c) Với (a = {1 over 2}) ta có hàm số: (y = {1 over 2}x)
Với a = -2 ta có hàm số : (y = – 2x)
*Vẽ đồ thị hàm số (y = {1 over 2}x)
Cho x = 0 thì y = 0 . Ta có: O(0;0)
Cho x = 2 thì y = 1 . Ta có: A(2;1)
Đồ thị hàm số (y = {1 over 2}x) đi qua O và A.
*Vẽ đồ thị hàm số y = -2x
Cho x = 0 thì y = 0. Ta có : O(0;0)
Cho x = 1 thì y = -2 . Ta có : B(1;-2)
Đồ thị hàm số y = -2x đi qua điểm O và B.
*Gọi A’, B’ lần lượt là hình chiếu của A, B trên Ox, Oy.
Ta có hai tam giác AA’O và BB’O có hai cạnh góc vuông tương ứng bằng nhau nên chúng bằng nhau.
Suy ra : (widehat {AOA’} = widehat {BOB’}) (1)
Vì ({rm{Ox}} bot {rm{Oy}}) nên (widehat {BOA’} + widehat {BOB’} = {90^0}) (2)
Từ (1) và (2) suy ra : (widehat {BOA’} + widehat {AOA’} = {90^0})
Vậy (OA bot OB) hay hai đường thẳng (y = {1 over 2}x) và y = -2x vuông góc với nhau.
Câu 26 trang 67 Sách Bài Tập (SBT) Toán 9 Tập 1
Cho hai đường thẳng
y = ax + b (d)
y = a’x + b’ (d’)
Chứng minh rằng :
Trên cùng một mặt phẳng tọa độ , hai đường thẳng (d) và (d’) vuông góc với nhau khi và chỉ khi a. a’ = 1.
Gợi ý làm bài:
Qua gốc tọa độ , kẻ đường thẳng y = ax // (d) và y = ax // (d’).
*Chứng mình (d) vuông góc với (d’) thì a. a’ = -1
Không mất tính tổng quát, giả sử a > 0
Khi đó góc tạo bởi tia Ox và đường thẳng y = ax là góc nhọn.
Suy ra góc tạo bởi tia Ox và đường thẳng y = a’x là góc tù ( vì các góc tạo bởi
đường thẳng y = ax và đường thẳng y = a’x với tia Ox hơn kém nhau ).
Suy ra: a’
Mà đường thẳng y = ax đi qua A(1;a), đường thẳng y = a’x đi qua B(1;a’)
nên đoạn AB vuông góc với Ox tại điểm H có hoành độ bằng 1.
Vì (left( {rm{d}} right) bot left( {{rm{d’}}} right)) nên hai đường thẳng y = ax và y = a’x vuông góc với nhau
Suy ra: (widehat {AOB} = {90^0})
Tam giác vuông AOB có (OH bot AB). Theo hệ thức lượng trong tam giác vuông ta có : (O{H^2} = HA.HB)
Hay: (a.left| {a’} right| = 1 Leftrightarrow a.left( { – a’} right) = 1 Leftrightarrow a.a’ = – 1)
Vậy nếu (d) vuông góc với (d’) thì a.a’ = -1
*Chứng minh 9a.a’ = – 1) thì (d) vuông góc với (d’)
Ta có : (a.a’ = – 1 Leftrightarrow a.left| {a’} right| = 1) hay (HA.HB = O{H^2})
Suy ra: ({{HA} over {OH}} = {{OH} over {HB}} Rightarrow widehat {OHA} = widehat {OHB} = {90^0})
Suy ra: (Delta OHA) đồng dạng (Delta BHO Rightarrow widehat {AOH} = widehat {OBH})
Mà (widehat {OBH} = widehat {BOH} = {90^0} Rightarrow widehat {AOH} = widehat {BOH} = {90^0})
Suy ra (OA bot OB) hay hai đường thẳng y = ax và y = a’x vuông góc với nhau hay (left( {rm{d}} right) bot left( {{rm{d’}}} right)).
Câu 27 trang 68 Sách Bài Tập (SBT) Toán 9 Tập 1
a) Vẽ trên cùng một mặt phẳng tọa độ đồ thị của các hàm số sau:
y = x (1)
y = 0,5x (2)
b) Đường thẳng (d) song song với trục Ox và cắt trục tung Oy tại điểm C
có tung độ bằng 2, theo thứ tự cắt các đường thẳng (1) và (2) tại D và E.
Tìm tọa độ của các điểm D, E . Tính chu vi và diện tích của tam giáo ODE.
Gợi ý làm bài:
a) * Vẽ đồ thị hàm số y = x
Cho x = 0 thì y = 0. Ta có : O(0;0)
Cho x = 1 thì y = 1. Ta có: A(1;1)
Đồ thị hàm số y = x đi qua O và A.
* Vẽ đồ thị hàm số y = 0,5x
Cho x = 0 thì y = 0.Ta có : O(0;0)
Cho x = 2 thì y = 1. Ta có : B(2;1)
Đồ thị hàm số y = 0,5x đi qua O và B .
b) Qua điểm C trên trục tung có tung độ bằng 2, kẻ đường thẳng song song với Ox
cắt đồ thị hàm số y = x tại D , cắt đồ thị hàm số y = 0,5x tại E.
Điểm D có tung độ bằng 2.
Thay giá trị y = 2 vào hàm số y = x ta được x = 2
Vậy điểm D(2;2)
Điểm E có tung độ bằng 2.
Thay giá trị y = 2 vào hàm số y = 0,5x ta được x = 4.
Vậy điểm E(4;2)
Gọi D’ và E’ lần lượt là hình chiều của D và E trên Ox.
Ta có: OD’ = 2, OE’ = 4.
Áp dụng định lý Pi-ta-go vào tam giác vuông ODD’, ta có:
(O{D^2} = OD{‘^2} + {rm{DD}}{‘^2} = {2^2} + {2^2} = 8)
Suy ra: (OD = sqrt 8 = 2sqrt 2 )
Áp dụng định lý Pi-ta-go vào tam giác vuông OEE’, ta có:
(O{E^2} = OE{‘^2}{rm{ + EE}}{{rm{‘}}^2} = {4^2} + {2^2} = 20)
Suy ra: (OE = sqrt {20} = 2sqrt 5 )
Lại có: (DE = CE – CD = 4 – 2 = 2)
Chu vi tam giác ODE bằng:
(eqalign{
& OD + DE + EO cr
& = 2sqrt 2 + 2 + 2sqrt 2 cr
& = 2left( {sqrt 2 + 1 + sqrt 5 } right) cr} )
Diện tích tam giác ODE bằng: ({1 over 2}DE.OC = {1 over 2}.2.2 = 2)
chinese.com.vn/giao-duc
Bạn đang đọc : Giải bài 25, 26, 27 trang 67, 68 SBT Toán 9 tập 1 2023 được cập nhập bởi Tekmonk.
Thông tin và kiến thức về chủ đề Giải bài 25, 26, 27 trang 67, 68 SBT Toán 9 tập 1 2023 do Học viện Công nghệ Tekmonk chọn lọc và tổng hợp cùng với các chủ đề liên quan khác.
Tham khảo thêm các khóa học công nghệ đỉnh cao tại: Học viện công nghệ Tekmonk 
Nguồn: Internet
Bạn đang tìm kiếm Giải bài 1, 2, 3, 4 trang 100 Vở
Bạn đang tìm kiếm Cảm nhận bài thơ Đoàn thuyền
Bạn đang tìm kiếm Vật lý 9 bài 25: Sự nhiễm từ
Bạn đang tìm kiếm 4 Đề đọc hiểu Đây thôn Vĩ
